Qualitative Spatial Reasoning
Diagrams and models seem inextricably linked with human spatial reasoning. Why? The wealth of concrete detail in such analog spatial representations at first might seem more than necessary for most spatial questions. Perhaps there are more abstract representations of shape and space that by themselves are sufficient for the tasks an intelligence cares about. If there are, then why don't people use them? Is it due to our highly evolved visual systems, whose computational power makes it cheaper to measure than to infer? Have we simply not discovered them yet? Or is there some deeper reason why humans rely so much on perception for spatial tasks?
We believe there are deep reasons for human reliance on perceptual abilties for spatial reasoning, and that these reasons dominate the structure of theories for spatial reasoning in both people or machines. Our concise statement of this idea is the Poverty Conjecture: There is no problem-independent, purely qualitative representation of space or shape. By "purely qualitative," we mean to rule out representations whose parts contain enough detailed information to permit calculation or the operation of perceptual-like processing. (Alas, we do not yet have a more precise definition.) Examples of descriptions that are purely qualitative include describing a two-dimensional shape by a list of signs of curvatures for boundary segments, or stating that two objects are gears that can mesh. Examples of descriptions that are quantitative enough to permit perception-like processes are symbolic descriptions with numerical components, high-resolution arrays, and symbolic algebraic expressions.
The MD/PV model
What does the poverty conjecture tell us about spatial reasoning? It suggests that spatial representations consist of two parts: a metric diagram, which includes quantitative information and thus provides a substrate that can support perceptual-like processing, and a place vocabulary, which makes explicit qualitative distinctions in shape and space relevant to the current task. The metric diagram can use floating-point numbers, algebra, or even high-precision arrays--whatever it uses, there must be enough detail to support answering spatial queries by calculation, and it must be capable of supporting the construction of place vocabularies. Place vocabularies consist of places, contiguous regions of space where some important property (e.g., in contact with a gear, inside a well) is constant. Computing the place vocabulary according to the needs of the problem ensures that the relevant distinctions are made. Defining the places in terms of elements in the metric diagram makes the diagram a good communication medium for diverse representations.
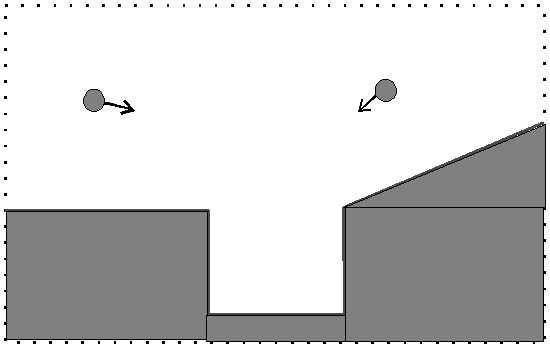
A FROB scenario. Can these balls collide? What if the right ball flies over
the well and the left ball falls into it? What if both balls fall into the well? Even
these simple qualitative stipulations can dramatically affect our judgments concerning
their fate.
FROB
Our first exploration of the MD/PV model was in a system that reasoned about motion through space, called FROB. FROB reasoned about the motion of balls bouncing around in a two-dimensional diagram. Aside from predicting the specific motion of a given ball, FROB also produced on-demand summaries of the eventual fate of a ball and estimates about whether two balls might collide. These problems are an important subset of the spatial reasoning tasks faced by any agent operating in a world of moving objects. For instance, one should be able to quickly figure out that two balls thrown into the same well might collide, while throwing the balls into different wells means they cannot collide, unless one of them escapes.
CLOCK
A more complex class of motion problems concerns fixed-axis mechanisms, such as mechanical clocks. The creation of reliable mechanical clocks was a milestone in mechanical engineering; thus the development of systems which can reason about such mechanisms serves as a good milestone for qualitative spatial reasoning. One milestone, the qualitative simulation of a mechanical clock from first principles, was achieved by our group in February 1988 with the CLOCK system built by Paul Nielsen and Boi Faltings as part of their Ph.D. theses.
CLOCK worked on fixed-axis mechanisms which could be decomposed into two-dimensional interactions. Given a CAD-like description of the parts of a mechanism and their degrees of freedom, CLOCK computed a place vocabulary based on configuration space. Configuration space is the appropriate basis for the place vocabulary because connectivity is central to kinematic state. Faltings developed an elegant characterization of such places and algorithms for computing them (Faltings, 1987, 1990). Instead of developing a single, massive high-dimensionality vocabulary, his algorithms created place vocabularies for pairs of parts that could interact, and used elements from these vocabularies to define kinematic states for the whole mechanism. The metric diagram plays a key role in this composition process, since defining consistent combinations of places sometimes requires projecting constraints from one vocabulary to another (and thus introducing new distinct places) when two vocabularies share a part.
CLOCK's metric diagram also played a key role in keeping envisioning tractable. Any diagram has noise, and the well-known sensitivity of kinematics to the details of surface shape means that smoothing the contours of a part in isolation is inappropriate. Nielsen realized that filtering at the level of the place vocabulary allows the interaction of the parts to be taken into account, and developed algorithms for removing "small" places and merging places that were "very close." The resulting simplification of the place vocabulary was dramatic: The number of potential kinematic states dropped from over 10,000 to 58 (Nielsen, 1989).
For qualitative reasoning about the dynamics of motion, Nielsen developed a qualitative vector algebra, and showed how shapes should be decomposed qualitatively to define robust notions of mechanical constraint. The requirements of reasoning about mechanical constraint again illustrate the need for interactions between qualitative and quantitative representations: The appropriate qualitative description of an object for figuring out how it can move if pushed depends not just on its shape, but also the qualitative direction to its center of rotation.
Integrating spatial reasoning with richer dynamical models
Many interesting physical systems, including internal combustion engines and pumps, can only be understood by comprehending the interactions of fluids and solid objects through motion. Recently Hyeonkyeong Kim has developed a set of qualitative representations and reasoning techniques that are sufficient for analyzing such examples. She developed a qualitative account of linkages that can envision up to four-bar linkages, showing that representing relative lengths of links, when combined with a qualitative representation of angle that includes both what quadrant it is in and relative inclination with respect to other links, suffices to solve this problem. She developed a qualitative method of computing streamline diagrams for laminar fluid flow, capable of generating explanations about how the Bernoulli effect generates lift over an airplane wing. Complex processes such as the combustion in a cylinder that drives a piston downward are typically approximated as instantaneous changes, so she developed a qualitative theory of impulses, showing how their effect could be modeled via structural changes in envisionments. Finally, figuring out how liquids can move inside containers that contain pistons and valves requires describing fluids in terms of their potential surface contacts. Kim developed such a representation for fluids, exploiting Nielsen's work on representing shapes and surfaces. Kim's research is a large step towards a comprehensive qualitative mechanics.
Reasoning About Graphs
Engineers commonly use graphs to express complex relationships, such as temperature-entropy or pressure-volume plots. Often these graphs are sketches, intended to convey qualitative information about the shapes of curves and relative magnitudes rather than precise numerical values. Using graphs makes sense for engineers and scientists because we have powerful perceptual apparatus that helps us decode them. Finding ways to make computers use graphs as easily and as flexibly as we do is a key problem in making software that can work better with people.
Yusuf Pisan has developed a system, called SKETCHY, that reasons about graphs. The input to SKETCHY is an annotated drawing consisting of lines, regions, and curves. Curves are approximated by a large set of very short line segments, which allows SKETCHY to process arbitrary-shaped curves. SKETCHY uses algorithms drawn from computer vision research to compute geometric properties and relationships. For instance, SKETCHY can infer from a temperature-entropy diagram for a substance that as temperature rises entropy does also in the superheat region.
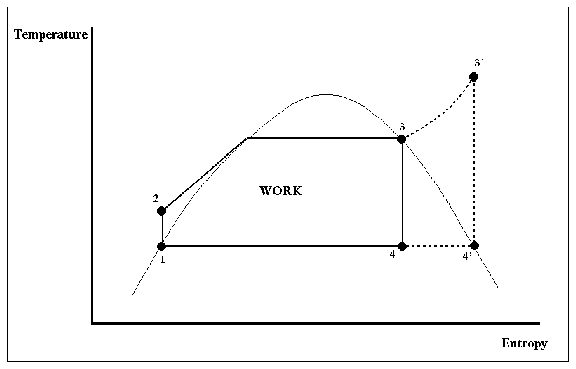
An important observation is that diagrams facilitate comparative analysis, that is, figuring out how a change in one parameter will affect another. Comparative analysis is important because it is at the heart of sensitivity analyses, which are crucial in design optimization, and because it provides a good way to check someone's understanding in training tasks. Comparative analysis can be done numerically, of course, but it is commonly used by engineers even when numerical data and models are not available. Purely qualitative theories of comparative analysis are very weak, almost certainly too weak to account for human capabilities. Casting comparative analysis questions as manipulations on diagrams allows people to use their perceptual apparatus to answer them. It is easier to see that superheating increases efficiency, for instance, if one looks at the projection of a steam cycle on a temperature-entropy diagram before and after superheat is added, and sees that the area under the curve (representing work output) has increased.
Selected Relevant Papers
Forbus, K. (August, 1980). Spatial and qualitative aspects of reasoning about motion. Proceedings of the National Conference on Artificial Intelligence. Stanford, California.
Forbus, K., Nielsen, P. and Faltings, B. (October, 1991). Qualitative Spatial Reasoning: The CLOCK Project. Artificial Intelligence, 51(1-3), 417-471.
Kim, H. (November, 1993). Qualitative reasoning about fluids and mechanics (Tech. Rep. No. 47). The Institute for the Learning Sciences, Northwestern University.
Pisan, Y. (1995). A visual routines based model of graph understanding. Proceedings of the 17th Annual conference of the Cognitive Science Society.
Relevant Projects
Qualitative Reasoning for Engineering Problem Solving
Back to Sketching page | Back to FQDT page | Back to Ideas page | Back to QRG Home Page